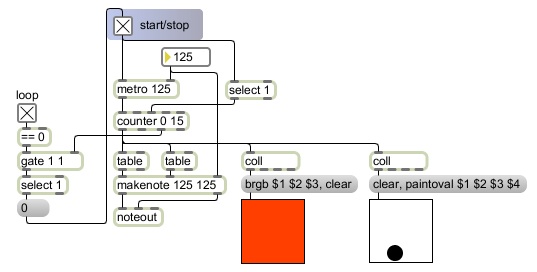
In all real world instances of randomness, we're not really talking about all possibilities; there is a limited range or field of possibilities. In a deck of cards, for instance, there are 52 possibilities (not counting jokers), each with a unique designation such as "three of hearts". So for each card there is a 1-in-52 chance of being the chosen card, and we know that it will have one of an expected set of designations. (There is no chance of, let's say, choosing a 57th card with the designation "seventeen of swords".) It is a limited number and type of possibility, but within those established limits randomness can occur.
True randomness is thus more of a concept than a reality. In computer programming, when we refer to random numbers, we actually mean pseudo-random numbers: numbers chosen from within a particular range of equally likely possibilities, by some system that is too complicated or obscure for us to comprehend, resulting in choices that appear to have no governing bias, method, or pattern. All programming languages contain a function for generating pseudo-random numbers--numbers within a particular range that appear to be completely unpredictable and to have no over-all pattern. (Mathematicians and computer scientists have devised many methods for generating pseudo-random numbers, but we won't concern ourselves here with the method of generation. We'll simply use the method provided for us by the programming language we happen to be using.)
Choosing a random number in a computer program (i.e., generating a number within a known set of possibilities by a pseudo-random process) is a way to simulate arbitrary decision making (a decision made without method or preference). It's also possible to program the computer to make arbitrary decisions using so-called weighted (i.e., unequal) probabilities, such that some numbers occur statistically more often than others (given a large enough statistical sample). We'll look at weighted randomness in another lesson. For now, we'll stick to random numbers of equal probability.
This program demonstrates some methods of random number generation in Max. It uses those random numbers to select sounds and images arbitrarily from limited sets of possibilities. For this program to work properly, you'll also need to download the very small audio clips and images that it uses. Just right-click (or control-click on Macintosh) on the following links, and save the files in the same directory as you save the program itself.
Images: gourmet.jpg, nubleu.jpg, brascroises.jpg, guitariste.jpg, tragedie.jpg, celestina.jpg
Sounds: bd.aif, tom.aif, snare.aif, hihat.aif, cymbal.aif
To begin discussing randomness in programming, let's stay with the "pick a card, any card" example for a moment. The key to the statistical definition of randomness, you'll recall, is that there is an equal likelihood of each possible outcome. In other words, there is an equal probability of each possible result. That leads us to the mathematical definition of probability: the number of looked-for results divided by the number of possible results. If we choose at random from 52 possibilities, there is a 1-in-52 chance of any particular looked-for result (such as the ace of spades, for example); that means the probability of choosing the ace of spades (1 looked-for result) out of all possible cards (52 of them) is 1/52, which is 0.019231. The probability of choosing any other particular card is the same. Note that by this definition of probability, the probability of any particular outcome (or set of looked-for results) can be expressed as a fraction from 0 to 1 inclusive, and the sum of the probabilities of all the possible results will equal 1.
If we put the chosen card back in the deck, and mix the cards up again, we'll once again have 52 cards, all of equal probability 0.019231. If on the other hand, we set the first chosen card aside instead of putting it back in the deck, and now choose from the remaining 51 cards, the first chosen card will now have a 0 probability of being chosen (it's no longer a possibility), and all the remaining cards will have a probability of 1/51, which is 0.019608. You can see that as we remove more cards from the deck, the probability of choosing any particular one of the remaining cards will increase, although all remaining cards will still have an equal probability. By the time we make our 51st choice, we'll be down to only two remaining cards, each with a probability of 0.5, and on the 52nd choice we'll have a 100% likelihood (a probability of 1) of choosing the one remaining card.
The distinction in the preceding paragraph between putting the chosen card back in the deck or not is an illustration of the difference between the random object and the urn object in Max. The random object chooses from a specified number of possible integers, with each choice being independent of any and all previous choices. The urn object also chooses at random, but it never repeats a choice; once it has chosen a certain number, that number is taken out of the set of possible choices (until the object is reset to its initial state with a clear message). Thus, urn avoids repetitions, and once it has chosen each possibility once, it stops choosing numbers, and instead sends a bang out its right outlet to report that all possible choices have been made. The random object, by contrast, always "forgets" its previous choice, and chooses anew from all of the numbers within the specified range.
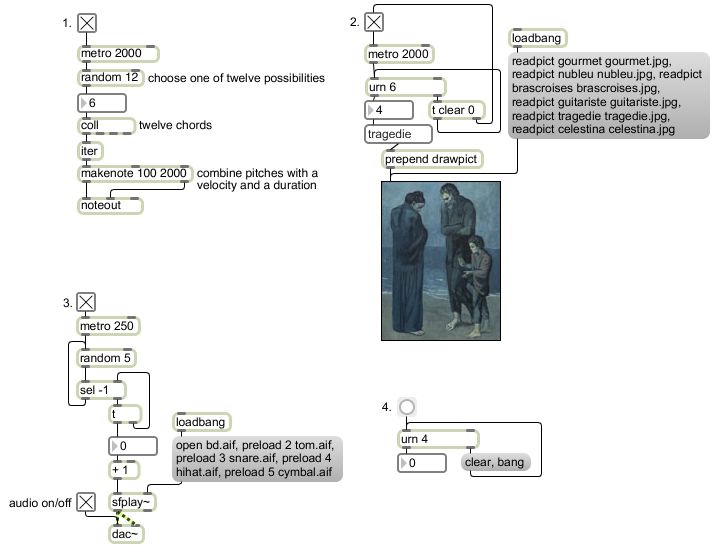
In this example program, program No. 1 chooses randomly from a list of twelve stored chords every two seconds. The chords are composed in such a way that they have a clear root and all can be reasonably interpreted to have a function in C minor, yet they are sufficiently ambiguous and are voiced in such a way that any chord can reasonably succeed any other chord.

Because the ordering of the chords is chosen at random--truly arbitrarily--by the program, the harmonic progression sounds rather aimless. That's because it is, in fact. The program has no sense of harmonic function, no rules about one chord leading to or following another, etc., the way that a human improviser would. So this type of arbitrary decision making at this formal level can't really be likened to compositional or improvisational decision making that a thinking human would perform. It's useful for producing unpredictable ordering of a set of events, though, and its effectiveness varies at different formal levels and with different types of controls and applications, so we'll see different uses of random numbers in future lessons.
The random object needs to be supplied with a number that specifies how many possible numbers it can choose from. Since this random object has the argument 12, it will choose from among 12 different numbers, integers 0 to 11. The random object always chooses numbers from 0 up to one less than the specified limit. This results in the right number of possibilities, and the fact that the range starts at 0 makes it useful for accessing arrays, as we've seen in earlier examples. It also means that we can easily change the range by adding some number to the output of random. Because each random choice is independent of previous choices there is a possibility--indeed there is a 0.083333 probability--that it will choose the same chord twice in a row.
The chords are stored as twelve 5-note lists in coll, indexed with numbers from 0 to 11. When these lists come out of coll they get broken up into five individual messages by iter so that they can be sent out as five separate--but essentially simultaneous--MIDI notes.
Program No. 2 uses urn to choose a random ordering of six images. Like the twelve chords, the images have been selected because they are related--they're all images of human subjects from Picasso's blue period--but there is no aesthetic or logical reasoning behind the order in which they're presented. The urn object ensures that there are no repetitions, and after it has chosen each of the six the possible numbers from 0 to 5, the next time it gets a bang from the metro it sends a bang out its right outlet to indicate that all possibilities have been expended. In this program, we use that notification to turn off the metro and to send a clear message back to urn to get it ready for the next time.
The program initially reads into memory each of the images we want to display, and assigns each of them a symbolic name. Those names are also stored in a umenu object so that they can be recalled with the numbers 0 through 5. When urn sends out a number, umenu uses the number to look up the name stored at that index in its internal array, and sends the name out its middle outlet. The prepend object puts the word drawpict before the name, so that a message such as drawpict guitariste will go to the lcd object and draw the picture.
Program No. 3 shows a slight variation on the sort of random selection used in No. 1. It plays very short sound files chosen at random from five possibilities, but never plays the same file twice in a row. Each time that a random number comes out, it goes to a select object to be compared to the previous number. If it is not the same as the previous number, it is passed out the right outlet of select and used to choose a sound. However, if it is the same as the previous number, select sends a bang back to random to try again. The select object is initialized with the argument -1 so that the first choice by random, which we know cannot be -1, will never be rejected. So after the very first choice, instead of there being five possibilities, there are actually only four, because we know that the preceding number will be rejected if it's chosen again immediately. It's still random, but with a rule imposed after the choice, a rule that rejects repetitions and keeps retrying until it gets a new number.
[N.B. This programming technique of using an object's output to potentially trigger immediate new input back to its left inlet is not generally advisable in Max, because it could cause a "stack overflow", a situation in which Max is required to perform too many tasks in too short a space of time. However, in this case, the probability that random would choose the same number enough times in a row to cause a stack overflow is minuscule.]
The program initially opens each of the different sound files we will want to play and stores a pointer to each of those files as a numbered "cue". Because of the way that the sfplay~ object is designed, the sound file most recently opened with an open message is considered cue number 1, and other numbered cues can be specified with the preload message. There is no cue number 0 in sfplay~; that number is reserved for stopping whatever cue is currently playing. Therefore, what we really need in order to access the five cues in sfplay~ is not numbers 0 through 4, but rather numbers 1 through 5. This is easy to achieve simply by adding 1 to every random number before passing it on to sfplay~ to be used as a cue number. (This addition is another example of an offset, as demonstrated in the earlier examples on linear mapping.)
Program No. 4 just demonstrates a handy trick for causing urn to keep outputting numbers once it has chosen all the possibilities. You can use the notification bang that comes out of urn's right outlet to trigger some new action, so in this example we use it to trigger a clear message back to urn itself, then retry with a new bang to urn. Note that this leaves open the possibility of a repetition between successive numbers, since the first new number that urn chooses after it is cleared could possibly be the same as the last number it chose before it was cleared. (The probability of an immediate repetition occurring in this way is inversely proportional to the number of possibilities.)
Notice that the complete randomness produced by random leaves open the possibility of some improbable successions of events occurring. Unlikely short-term patterns, such as 2,2,2 or 1,2,1,2 are possible, especially when the total number of possibilities is relatively small. So random is useful for generating unpredictable results, but that includes the possibility of improbable distinctive successions. The urn object avoids such successions that involve repetition of a number, but it becomes more predictable as its number of possible choices decreases. (We know that it won't choose a number that it has already chosen.)
The artist-programmer should determine what sort of randomness, if any, meets the aesthetic goals of a particular situation. Future lessons will show other uses of random numbers for decision making.


.jpg)